Психиатрия Психиатрия и психофармакотерапия им. П.Б. Ганнушкина
Психиатрия Психиатрия и психофармакотерапия им. П.Б. Ганнушкина
№03 2017
Метод определения пороговых критериев в клинических рейтинговых шкалах, разработанных на основе модели Раша №03 2017
Номера страниц в выпуске:19-24
В статье описан метод определения пороговых оценочных критериев клинических рейтинговых шкал, разработанных на основе модели Раша. Методика определения пороговых оценок показана на примере модифицированной шкалы оценки депрессии Гамильтона. Разработанные на основе модели Раша пороговые критерии характеризуются высокой стабильностью и согласованностью с клиническими данными. Новые оценочные критерии модифицированной шкалы Гамильтона значительно превосходят по диагностической эффективности пороговые критерии оригинальной шкалы Гамильтона.
Метод определения пороговых критериев в клинических рейтинговых шкалах, разработанных на основе модели Раша
М.А.Ассанович
УО «Гродненский государственный медицинский университет». 230009, Республика Беларусь, Гродно, ул. Горького, д. 80
70malas@gmail.com
В статье описан метод определения пороговых оценочных критериев клинических рейтинговых шкал, разработанных на основе модели Раша. Методика определения пороговых оценок показана на примере модифицированной шкалы оценки депрессии Гамильтона. Разработанные на основе модели Раша пороговые критерии характеризуются высокой стабильностью и согласованностью с клиническими данными. Новые оценочные критерии модифицированной шкалы Гамильтона значительно превосходят по диагностической эффективности пороговые критерии оригинальной шкалы Гамильтона.
Ключевые слова: модель Раша, модифицированная шкала оценки депрессии Гамильтона, пороговые критерии.
Для цитирования: Ассанович М.А. Метод определения пороговых критериев в клинических рейтинговых шкалах, разработанных на основе модели Раша. Психиатрия и психофармакотерапия. 2017; 19 (3): 19–24.
The method of defining cut-off criteria in clinical rating scales developed using Rasch model
M.A.Assanovich
Grodno State Medical University. 230009, Republic of Belarus, Grodno, ul. Gorkogo, d. 80
70malas@gmail.com
The article describes the method of defining cut-off criteria of clinical rating scales developed using Rasch model. Method of determining cut-off criteria is shown in example of modified version of the Hamilton Depression Rating Scale. Cut-off criteria developed on the basis of Rasch model are characterized by high level of stability and consistency with clinical data. New cut-off criteriaof modified version of the Hamilton scale are far superior to diagnostic efficiency of the cut-off criteria of the original Hamilton scale.
Key words: Rasch model, modified version of the Hamilton Depression Rating Scale, cut-off criteria.
For citation: Assanovich M.A. The method of defining cut-off criteria in clinical rating scales developed using Rasch model. Psychiatry and Psychopharmacotherapy. 2017; 19 (3): 19–24.
Введение
Психометрические рейтинговые шкалы широко применяются в психиатрии. Чаще всего они используются для оценки выраженности психопатологической симптоматики у пациентов в процессе фармакотерапии. Результаты исследования с помощью рейтинговых шкал также полезны для точной квалификации тяжести состояния пациента и определения прогноза в динамике проводимой терапии [1].
Учитывая выполняемые диагностические функции, каждая клиническая психометрическая шкала должна соответствовать требованиям объективного, надежного и точного измерения. Одним из актуальных аспектов практического применения рейтинговых шкал является наличие обоснованных и валидных критериев оценки выраженности измеряемого конструкта. Данные критерии представляют собой пороговые оценки шкалы, образующие границы различных диапазонов выраженности измеряемого конструкта. Суммарные оценки шкалы, принадлежащие одному и тому же метрическому диапазону, отражают один и тот же уровень выраженности конструкта и одинаково интерпретируются [2].
В настоящее время в клинической психометрике существует 2 способа определения критериев интерпретации. Первый способ основан на внешнем критерии. Второй способ включает методы, основанные на распределении и стандартной ошибке измерения [2].
Первый способ выделения критериев интерпретации требует наличия изначально заданного внешнего критерия. В качестве внешнего критерия выбирается легко клинически интерпретируемый и откалиброванный фактор. Формируются 2 выборки испытуемых по принципу «случай–контроль». Испытуемые 1-й группы характеризуются наличием данного фактора, у испытуемых 2-й группы он отсутствует. Затем проводится ROC-анализ (Receiver Operating Characteristic) и рассчитывается отсекающее значение, которое и является критерием интерпретации. Отсекающее значение определяется по индексу Юдена (Yuden), максимизирующему сумму значений сенситивности и специфичности. В качестве внешнего критерия могут использоваться оценки экспертов, другие методики, имеющие статус «золотого стандарта». Например, с помощью экспертных оценок клиницистов можно сформировать
3 группы пациентов: с легкой, умеренной и значительной выраженностью конструкта. Далее после проведения ROC-анализа для 2 смежных групп определяются оценки, дифференцирующие 3 степени выраженности конструкта. Эти оценки и будут являться критериями интерпретации результатов исследования [2].
Недостатками подхода, использующего внешний критерий, являются зависимость критерия от субъективных оценок, особенностей популяции, нестабильность, отсутствие связи критериев интерпретации с измерительными свойствами психодиагностической методики.
Второй способ определения критериев интерпретации основан на параметрах распределения (дисперсии оценок) [2].
В ряде работ эмпирически показано, что разница между оценками, составляющая 0,5 стандартного отклонения, соответствует минимальным статистически значимым различиям между этими оценками. В других работах приводятся данные, что о минимальных статистически значимых различиях свидетельствует разница между оценками, равная одному стандартному отклонению. Величина стандартного отклонения от средней оценки представляет собой условную и недостаточно обоснованную меру определения критериев интерпретации. Использование стандартного отклонения требует нормального распределения конструкта в популяции, что является редким явлением в клинической психодиагностике. Величина стандартного отклонения зависит от особенностей популяции, поэтому определенные на ее основе критерии интерпретации отличаются нестабильностью и имеют невысокую точность [2].
В последние годы в клинической психометрике стали активно использоваться новые подходы к построению и оценке диагностической эффективности клинических рейтинговых шкал. Одним из наиболее перспективных подходов является метрический анализ на основе модели Раша [3]. Модель Раша позволяет создать психометрическую шкалу, соответствующую таким принципам научного измерения, как аддитивность и инвариантность. В отличие от других способов конструирования психодиагностических шкал метрическая шкала Раша характеризуется стабильностью, независимостью от особенностей популяции, имеет равноинтервальную калибровку. Методологический аппарат метрической системы Раша дает возможность оценить конструктную валидность каждого диагностического пункта, рассчитать статистику надежности.
В результате реализации модели создается равноинтервальная шкала, в которой каждой общей оценке соответствует своя мера выраженности измеряемого конструкта, представленная в логитах. Расстояния между оценками на шкале соответствуют принципам аддитивной структуры и отражают метрические отношения между различными уровнями выраженности конструкта. В метрической системе Раша конструируется шкала, которая наиболее правдоподобно подходит для измерения данного психологического конструкта. Распределение оценок в этой шкале не зависит от свойств популяции [4].
Применительно к теме настоящей работы метрическая шкала Раша имеет важную особенность, позволяющую с высокой точностью определить пороговые критерии оценки выраженности измеряемого конструкта. Эта особенность заключается в том, что для каждой оценки по шкале, выраженной в логитах, рассчитывается индивидуальная ошибка измерения [5].
Цель настоящего исследования состояла в методологическом обосновании и оценке клинической валидности критериев оценки выраженности психопатологического конструкта, разработанных на основе модели Раша.
Методология исследования
В качестве психометрической шкалы была выбрана модифицированная нами на основе модели Раша шкала оценки депрессии Гамильтона (Hamilton Rating Scale for Depression – HDRS). Модифицированная шкала (HDRSm-10), разработанная на основе модели Раша и включающая 10 диагностических пунктов, характеризуется удовлетворительными психометрическими свойствами, значительно превосходящими таковые у оригинальной шкалы HDRS. Все пункты шкалы имеют адекватную конструктную валидность и оценивают выраженность депрессии на всем континууме шкалы. Модифицированная шкала имеет одномерную структуру и высокие показатели надежности и дискриминативности [6].
Первичные данные включали протоколы исследования с помощью HDRSm-10 пациентов с легкой, умеренной и тяжелой степенями депрессии, а также здоровых участников исследования.
Пациенты с легким депрессивным эпизодом проходили амбулаторное лечение. Пациенты с умеренным и тяжелым депрессивным эпизодом находились на стационарном лечении. Все пациенты проходили обследование на базе Гродненского областного клинического центра «Психиатрия–наркология» и Гродненской городской клинической больницы №3. Психодиагностическое обследование проводилось в течение первых 5 дней после выставления клинического диагноза. Для сравнительного анализа были сформированы 3 выборки первичных данных. Выборка 1 состояла из данных исследования группы участников из 551 человека. Группа включала здоровых лиц и пациентов с клинически верифицированным диагнозом депрессии разной степени тяжести. Возраст участников исследования составил 23–54 года, из них 231 мужчина и 320 женщин. Выборка 2 состояла из данных исследования новой группы участников в числе 333 человек. Группа участников исследования включала здоровых лиц и пациентов с клинически верифицированным диагнозом депрессии разной степени тяжести. Возраст участников составил 24–53 года, из них 145 мужчин и 189 женщин.
Методология определения пороговых критериев выраженности депрессии в шкале HDRSm-10 состояла в следующем.
Поскольку клиническая психометрическая шкала направлена на измерение латентного психопатологического конструкта, измерение последнего всегда включает случайную ошибку. При многократных исследованиях одного и того же участника исследования значения полученных оценок будут отличаться друг от друга в диапазоне, который определяется случайной ошибкой измерения. Случайная ошибка в каждом очередном исследовании также принимает неодинаковые значения, образуя дисперсию ошибки s2error [7].
Стандартное отклонение случайной ошибки получило название стандартной ошибки измерения (SEM): √s2error (1), где s2error – дисперсия случайной ошибки [7].
Разделение шкалы на значимые метрические уровни, границы которых образуют пороговые критерии, основывается на определении статистически значимых метрических различий между шкальными оценками. Если оценки метрически различаются, они относятся к различным метрическим уровням выраженности конструкта и являются научно обоснованными критериями их интерпретации. Если оценки статистически не различаются, то они соответствуют одному и тому же метрическому уровню выраженности конструкта, и, следовательно, их критерии интерпретации одинаковы. Статистические различия между оценками определяются с помощью стандартной ошибки разницы между ними (SEMdif) c заданным уровнем вероятности. Значение SEMdif рассчитывается на основе значения SEM каждой из оценок, между которыми определяется разница.
Пусть нам необходимо определить стандартную ошибку разницы между любыми 2 шкальными оценками Xi и Хj. Каждая оценка представляет собой переменную, принимающую различные значения при многократных исследованиях в диапазоне, образуемом своей стандартной ошибкой измерения: SEMXi для оценки Xi и SEMXj для оценки Хj. Разность между этими оценками (Хj - Хi) также представляет собой переменную, значение которой изменяется при многократных исследованиях в диапазоне стандартной ошибки разности между этими оценками (SEMXj-Xi). Задача состоит в определении значения SEMXj-Xi. Поскольку SEM представляет собой стандартное отклонение случайной ошибки шкальной оценки, то SEMXj-Xi является стандартным отклонением случайной ошибки разности между шкальными оценками Xi и Хj: SEMXj-Xi = √s2error (Xj-Xi) (2), где s2error (Xj-Xi) – дисперсия случайной ошибки разности оценок Xi и Хj. Как известно, дисперсия разности 2 переменных равна сумме дисперсий этих 2 переменных. Следовательно, формула расчета дисперсии ошибки разности оценок Xi и Хj будет иметь вид: s2error (Xj-Xi) = s2error (Xi) + s2error (Xj) (3). Отсюда значение SEMXj-Xi можно определить по формуле: SEMXj-Xi = √s2error (Xj-Xi) = √s2error (Xi) + s2error (Xj) = √SEM2Xi + SEM2Xj(4). Таким образом, стандартная ошибка разности 2 оценок равна квадратному корню суммы квадратов стандартных ошибок измерения каждой из этих оценок. Следовательно, для расчета стандартной ошибки разности между оценками (SEMdif) достаточно знать значения стандартных ошибок измерения этих оценок (SEM).
Итак, если разность между оценками с приемлемым уровнем статистической значимости превышает величину стандартной ошибки этой разницы, то с высокой долей вероятности можно утверждать о принадлежности данных оценок разным уровням выраженности измеряемого конструкта. Приемлемый уровень статистической значимости определяется допустимой вероятностью отвержения нулевой гипотезы. В данном случае нулевая гипотеза состоит в том, что статистически значимое превышение разности 2 оценок над величиной стандартной ошибки измерения этой разности не будет свидетельствовать о действительных различиях между оценками. В исследованиях, посвященных разработке критериев интерпретации, для определения уровня статистической значимости различий между оценками эмпирически принята вероятность, равная 95% [2]. Распределение случайной ошибки подчиняется нормальному закону. Это дает возможность использования значений стандартизованных Z-оценок в качестве критериев статистической значимости разности между оценками. Каждому значению плотности вероятности соответствует определенная Z-оценка. Для вероятности 95% значение Z-оценки равно 1,96 [2]. Таким образом, разность между 2 шкальными оценками Xi и Хj будет статистически значимой, если соблюдается следующее условие:
Xj-Xi/√SEM2Xi+SEM2Xj >1,96. (5). Преобразуем данное выражение в более удобную форму: Xj-Xi>1,96√SEM2Xi+SEM2Xj (6). Выражение (6) можно определить как метрическое условие, определяющее принадлежность 2 шкальных оценок к статистически разным метрическим уровням с 95% вероятностью. Практическое использование данного метрического условия на основе модели Раша проводится следующим образом. Как мы уже отмечали выше, в ходе психометрического анализа в метрической системе Раша строится равноинтервальная шкала, на которой каждая суммарная оценка имеет свою метку, выраженную в логитах. Для каждой метки рассчитывается индивидуальная ошибка измерения. Метрическое условие (6) используется для разделения шкалы логитов на метрические уровни. Логиты, образующие границы уровней, являются пороговыми критериями. Каждому критерию, выраженному в логитах, соответствует определенная суммарная оценка. Процесс разделения шкалы на уровни проводится, начиная с метки шкалы, эквивалентной нулевой суммарной оценке. Данная метка соответствует оценке Xi в метрическом условии. Далее условие последовательно проверяется для каждой последующей метки шкалы. При этом в правую часть неравенства подставляются значения соответствующих ошибок измерения. Как только значение левой части неравенства станет больше правой, первый метрический уровень определен. При этом суммарная оценка шкалы, эквивалентная метке шкалы, выступающей в качестве оценки Xj, будет определена как нижний пороговый критерий 2-го метрического уровня. Предшествующая ей оценка представляет верхний пороговый критерий 1-го уровня. Далее в метрическое условие в качестве оценки Xi подставляется метка шкалы, образовавшая нижний пороговый критерий 2-го метрического уровня, и процесс повторяется до самой последней метки, которая эквивалентна максимальной суммарной оценке по шкале.
Клиническая верификация пороговых метрических критериев проводилась путем статистического анализа таблиц сопряженности клинических и метрических критериев. При этом строки таблицы включали частоты клинических критериев выраженности конструкта по Международной классификации болезней 10-го пересмотра (МКБ-10), столбцы таблицы содержали частоты метрических критериев. В ячейках на пересечении строк и столбцов локализовались совпадающие частоты. Статистический анализ заключался в определении максимальной частоты каждого клинического критерия, которая совпадала с максимальной частотой определенного метрического критерия. Метрический критерий, совпавший по максимальной частоте с определенным внешним клиническим критерием, приобретал свойство клинической интерпретируемости, соответствующий данному внешнему критерию. Если внешнему клиническому критерию по максимальным частотам соответствовали 2 и более метрических критерия, то они объединялись в один общий критерий, имеющий 2 метрических уровня. В качестве статистических критериев определения значимой максимальной частоты использовался точный метод Фишера (ТМФ) [8].
Оценка диагностической эффективности пороговых критериев осуществлялась путем оценки степени согласованности классификации испытуемых по степени тяжести депрессии, выполненной на основе метрических критериев, с классификацией, построенной на основе клинических критериев МКБ-10. Оценка степени соответствия классификаций проводилась с помощью статистических критериев c2, процента рассогласованности классификаций, индекса каппа Коэна, индекса выраженности эффекта (effect-size) V Крамера [9]. Оценка эффективности критериев классификации проводилась на данных исследования выборки 1 и выборки 2. Оцениванию подвергались новые критерии интерпретации в сравнении с существующими критериями оригинальной 17-пунктовой шкалы HRSD. Для проведения сравнительного анализа использовались 2 набора оригинальных пороговых критериев. Первый набор состоял из традиционных устоявшихся пороговых оценок, второй набор включал пороговые оценки, рекомендуемые Американской психиатрической ассоциацией (American Psychiatric Association – APA) [10]. Пороговые критерии обоих наборов представлены в табл. 1.

Результаты
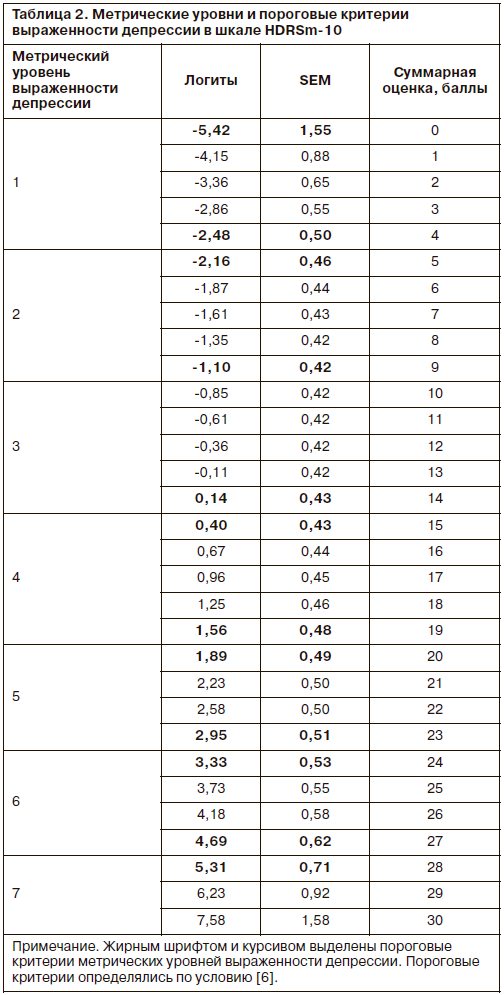 В табл. 2 представлены все оценки шкалы HDRSm-10, разделенные на метрические уровни.
В табл. 2 представлены все оценки шкалы HDRSm-10, разделенные на метрические уровни.
Как следует из данных табл. 2, в шкале HDRSm-10 на основе модели Раша выделяются 7 метрических уровней. Это означает, что данная шкала с 95% вероятностью дифференцирует 7 степеней выраженности депрессии. Метрические уровни на схеме расположены последовательно сверху вниз и отражают возрастающие степени выраженности депрессии.
Эффективное практическое применение модифицированной шкалы HDRSm-10 требует согласования метрических критериев выраженности депрессии с внешними клиническими критериями. Клиническая валидизация метрических критериев интерпретации проводилась с помощью статистического анализа таблиц сопряженности классификации участников исследования на основе внешнего клинического критерия (по МКБ-10) и с классификацией на основе метрических критериев шкалы HDRSm-10. В табл. 3 представлены частоты метрических уровней, определенных в модифицированной шкале HDRSm-10, в сопряжении с частотами клинических уровней в группах участников.
Исходя из практической целесообразности, метрические и клинические уровни должны быть согласованы таким образом, чтобы каждый метрический уровень соответствовал только одному клиническому. Это обеспечивает понятность и удобство интерпретации метрических критериев с клинической точки зрения. Как следует из анализа данной таблицы, в каждом столбце обнаруживается частота, имеющая максимальное значение. Это означает, что каждый метрический уровень эквивалентен только одному клиническому уровню.
Анализ данных табл. 3 позволяет выполнить согласование метрических и клинических уровней, представленных в табл. 2. Первый метрический уровень (от 0 до 4 баллов) соответствует уровню отсутствия депрессии. Второй метрический уровень (от 5 до 9 баллов) согласуется с легкой степенью депрессии. Третий (10–14 баллов) и четвертый (15–19 баллов) метрические уровни соответствуют средней степени тяжести депрессии, установленной по клиническому критерию. Последние 3 метрических уровня (20–23, 24–27, 28 и более баллов) эквивалентны клинически диагностируемой тяжелой степени депрессии.
Таким образом, метрические критерии шкалы HDRSm-10, определенные на основе модели Раша, эффективно согласуются с клиническими уровнями выраженности депрессии. При этом клинический уровень умеренно выраженной депрессии включает 2 метрически и статистически отличающихся друг от друга подуровня. Клинический уровень тяжелой депрессии включает 3 дифференцированных метрических подуровня. Наличие нескольких метрических уровней в рамках одного клинического позволяет точнее и валиднее оценивать изменение выраженности депрессии в динамике терапии.
Сравнительная оценка диагностической эффективности оригинальных и новых критериев интерпретации проводилась на основе определения степени согласованности критериев оригинальной и модифицированной шкал с клиническими критериями оценки тяжести депрессии в соответствии с МКБ-10. Для оценки степени согласованности использовались следующие статистические критерии: c2, индекс V Крамера, показатель рассогласованности в процентах, индекс Каппа. Оценка диагностической эффективности проводилась дважды на разных выборках данных (выборка 1 и выборка 2). Значения показателей диагностической эффективности представлены в табл. 4. В процессе оценки эффективности критериев шкалы HDRSm-10 несколько метрических уровней, эквивалентных одному и тому же клиническому уровню (см. табл. 3), объединялись в данный клинический уровень. В частности, третий и четвертый метрические уровни были объединены в один уровень умеренной степени тяжести депрессии, четвертый, пятый и шестой метрические уровни объединены в один уровень тяжелой степени депрессии. Первый и второй метрические уровни представляли соответственно уровень отсутствия депрессии и легкую степень депрессии.
Оценка показателей, приведенных в табл. 4, обнаруживает выраженные различия в диагностической эффективности пороговых критериев оригинальной шкалы HDRS и критериев модифицированной шкалы. Пороговые критерии оригинальной шкалы показали выраженную рассогласованность с клиническими критериями МКБ-10. Степень рассогласования традиционных критериев с клиническими данными в обеих выборках превышает 40%, критериев АРА – от 30 до 38%. Отмечаются достоверные различия по критерию c2 в обеих выборках (p<0,0001). Эффект различий (effect-size) между классификациями по значениям индекса V Крамера составил высокую степень выраженности. Значения коэффициента Каппа для критериев оригинальной шкалы также соответствуют невысокой согласованности с клиническими критериями. Полученные данные свидетельствуют о низкой диагностической эффективности как традиционных, так и рекомендованных АРА пороговых критериев оценки тяжести депрессии оригинальной шкалы HDRS.
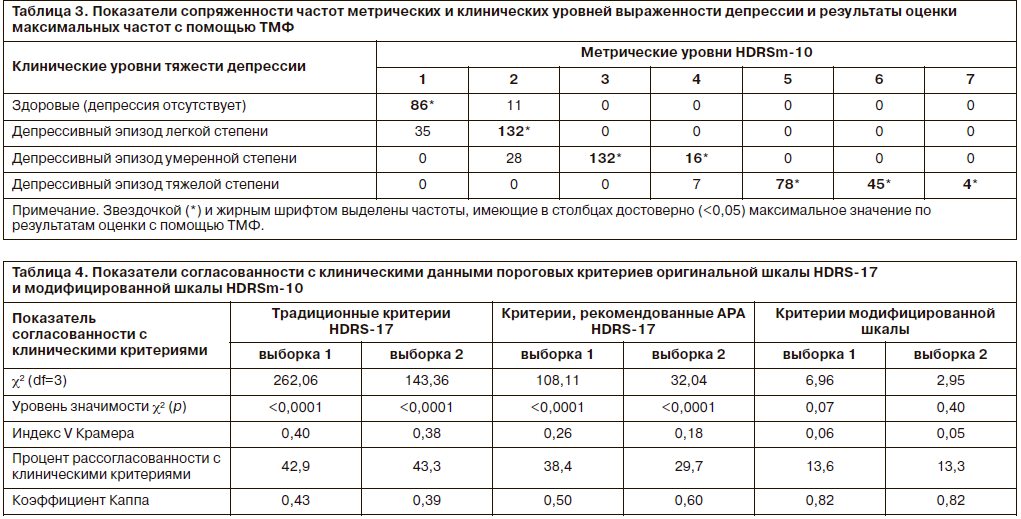
Критерии модифицированной шкалы, напротив, показали высокую эффективность при сопоставлении с клиническими критериями. Степень рассогласования с клиническими данными составляет менее 14%. Значения индекса Каппа отражают достаточно высокий уровень согласованности. Значения критерия c2 обнаруживают отсутствие достоверных различий с классификацией по клиническим критериям в обеих выборках. Значения индекса выраженности эффекта V (effect-size) свидетельствуют о слабой рассогласованности в выборке 1 (V=0,06) и об отсутствии таковой в выборке 2 (V=0,05).
Таким образом, на основании проведенного исследования можно сделать следующие выводы.
1. Метрические пороговые критерии оценки психопатологического конструкта, разработанные на основе модели Раша, обладают высокой степенью стабильности и воспроизводимости, эффективно согласуются с клиническими данными.
2. Разработанная нами на основе модели Раша модифицированная шкала оценки депрессии HDRSm позволяет оценить 7 метрических уровней выраженности депрессии, хорошо согласуется с клиническими данными и значительно превосходит по своим диагностическим свойствам оригинальную шкалу HRSD.
Сведения об авторе
Ассанович Марат Алиевич – канд. мед. наук, доц., зав. каф. медицинской психологии и психотерапии ГрГМУ.
E-mail: 70malas@gmail.com
М.А.Ассанович
УО «Гродненский государственный медицинский университет». 230009, Республика Беларусь, Гродно, ул. Горького, д. 80
70malas@gmail.com
В статье описан метод определения пороговых оценочных критериев клинических рейтинговых шкал, разработанных на основе модели Раша. Методика определения пороговых оценок показана на примере модифицированной шкалы оценки депрессии Гамильтона. Разработанные на основе модели Раша пороговые критерии характеризуются высокой стабильностью и согласованностью с клиническими данными. Новые оценочные критерии модифицированной шкалы Гамильтона значительно превосходят по диагностической эффективности пороговые критерии оригинальной шкалы Гамильтона.
Ключевые слова: модель Раша, модифицированная шкала оценки депрессии Гамильтона, пороговые критерии.
Для цитирования: Ассанович М.А. Метод определения пороговых критериев в клинических рейтинговых шкалах, разработанных на основе модели Раша. Психиатрия и психофармакотерапия. 2017; 19 (3): 19–24.
The method of defining cut-off criteria in clinical rating scales developed using Rasch model
M.A.Assanovich
Grodno State Medical University. 230009, Republic of Belarus, Grodno, ul. Gorkogo, d. 80
70malas@gmail.com
The article describes the method of defining cut-off criteria of clinical rating scales developed using Rasch model. Method of determining cut-off criteria is shown in example of modified version of the Hamilton Depression Rating Scale. Cut-off criteria developed on the basis of Rasch model are characterized by high level of stability and consistency with clinical data. New cut-off criteriaof modified version of the Hamilton scale are far superior to diagnostic efficiency of the cut-off criteria of the original Hamilton scale.
Key words: Rasch model, modified version of the Hamilton Depression Rating Scale, cut-off criteria.
For citation: Assanovich M.A. The method of defining cut-off criteria in clinical rating scales developed using Rasch model. Psychiatry and Psychopharmacotherapy. 2017; 19 (3): 19–24.
Введение
Психометрические рейтинговые шкалы широко применяются в психиатрии. Чаще всего они используются для оценки выраженности психопатологической симптоматики у пациентов в процессе фармакотерапии. Результаты исследования с помощью рейтинговых шкал также полезны для точной квалификации тяжести состояния пациента и определения прогноза в динамике проводимой терапии [1].
Учитывая выполняемые диагностические функции, каждая клиническая психометрическая шкала должна соответствовать требованиям объективного, надежного и точного измерения. Одним из актуальных аспектов практического применения рейтинговых шкал является наличие обоснованных и валидных критериев оценки выраженности измеряемого конструкта. Данные критерии представляют собой пороговые оценки шкалы, образующие границы различных диапазонов выраженности измеряемого конструкта. Суммарные оценки шкалы, принадлежащие одному и тому же метрическому диапазону, отражают один и тот же уровень выраженности конструкта и одинаково интерпретируются [2].
В настоящее время в клинической психометрике существует 2 способа определения критериев интерпретации. Первый способ основан на внешнем критерии. Второй способ включает методы, основанные на распределении и стандартной ошибке измерения [2].
Первый способ выделения критериев интерпретации требует наличия изначально заданного внешнего критерия. В качестве внешнего критерия выбирается легко клинически интерпретируемый и откалиброванный фактор. Формируются 2 выборки испытуемых по принципу «случай–контроль». Испытуемые 1-й группы характеризуются наличием данного фактора, у испытуемых 2-й группы он отсутствует. Затем проводится ROC-анализ (Receiver Operating Characteristic) и рассчитывается отсекающее значение, которое и является критерием интерпретации. Отсекающее значение определяется по индексу Юдена (Yuden), максимизирующему сумму значений сенситивности и специфичности. В качестве внешнего критерия могут использоваться оценки экспертов, другие методики, имеющие статус «золотого стандарта». Например, с помощью экспертных оценок клиницистов можно сформировать
3 группы пациентов: с легкой, умеренной и значительной выраженностью конструкта. Далее после проведения ROC-анализа для 2 смежных групп определяются оценки, дифференцирующие 3 степени выраженности конструкта. Эти оценки и будут являться критериями интерпретации результатов исследования [2].
Недостатками подхода, использующего внешний критерий, являются зависимость критерия от субъективных оценок, особенностей популяции, нестабильность, отсутствие связи критериев интерпретации с измерительными свойствами психодиагностической методики.
Второй способ определения критериев интерпретации основан на параметрах распределения (дисперсии оценок) [2].
В ряде работ эмпирически показано, что разница между оценками, составляющая 0,5 стандартного отклонения, соответствует минимальным статистически значимым различиям между этими оценками. В других работах приводятся данные, что о минимальных статистически значимых различиях свидетельствует разница между оценками, равная одному стандартному отклонению. Величина стандартного отклонения от средней оценки представляет собой условную и недостаточно обоснованную меру определения критериев интерпретации. Использование стандартного отклонения требует нормального распределения конструкта в популяции, что является редким явлением в клинической психодиагностике. Величина стандартного отклонения зависит от особенностей популяции, поэтому определенные на ее основе критерии интерпретации отличаются нестабильностью и имеют невысокую точность [2].
В последние годы в клинической психометрике стали активно использоваться новые подходы к построению и оценке диагностической эффективности клинических рейтинговых шкал. Одним из наиболее перспективных подходов является метрический анализ на основе модели Раша [3]. Модель Раша позволяет создать психометрическую шкалу, соответствующую таким принципам научного измерения, как аддитивность и инвариантность. В отличие от других способов конструирования психодиагностических шкал метрическая шкала Раша характеризуется стабильностью, независимостью от особенностей популяции, имеет равноинтервальную калибровку. Методологический аппарат метрической системы Раша дает возможность оценить конструктную валидность каждого диагностического пункта, рассчитать статистику надежности.
В результате реализации модели создается равноинтервальная шкала, в которой каждой общей оценке соответствует своя мера выраженности измеряемого конструкта, представленная в логитах. Расстояния между оценками на шкале соответствуют принципам аддитивной структуры и отражают метрические отношения между различными уровнями выраженности конструкта. В метрической системе Раша конструируется шкала, которая наиболее правдоподобно подходит для измерения данного психологического конструкта. Распределение оценок в этой шкале не зависит от свойств популяции [4].
Применительно к теме настоящей работы метрическая шкала Раша имеет важную особенность, позволяющую с высокой точностью определить пороговые критерии оценки выраженности измеряемого конструкта. Эта особенность заключается в том, что для каждой оценки по шкале, выраженной в логитах, рассчитывается индивидуальная ошибка измерения [5].
Цель настоящего исследования состояла в методологическом обосновании и оценке клинической валидности критериев оценки выраженности психопатологического конструкта, разработанных на основе модели Раша.
Методология исследования
В качестве психометрической шкалы была выбрана модифицированная нами на основе модели Раша шкала оценки депрессии Гамильтона (Hamilton Rating Scale for Depression – HDRS). Модифицированная шкала (HDRSm-10), разработанная на основе модели Раша и включающая 10 диагностических пунктов, характеризуется удовлетворительными психометрическими свойствами, значительно превосходящими таковые у оригинальной шкалы HDRS. Все пункты шкалы имеют адекватную конструктную валидность и оценивают выраженность депрессии на всем континууме шкалы. Модифицированная шкала имеет одномерную структуру и высокие показатели надежности и дискриминативности [6].
Первичные данные включали протоколы исследования с помощью HDRSm-10 пациентов с легкой, умеренной и тяжелой степенями депрессии, а также здоровых участников исследования.
Пациенты с легким депрессивным эпизодом проходили амбулаторное лечение. Пациенты с умеренным и тяжелым депрессивным эпизодом находились на стационарном лечении. Все пациенты проходили обследование на базе Гродненского областного клинического центра «Психиатрия–наркология» и Гродненской городской клинической больницы №3. Психодиагностическое обследование проводилось в течение первых 5 дней после выставления клинического диагноза. Для сравнительного анализа были сформированы 3 выборки первичных данных. Выборка 1 состояла из данных исследования группы участников из 551 человека. Группа включала здоровых лиц и пациентов с клинически верифицированным диагнозом депрессии разной степени тяжести. Возраст участников исследования составил 23–54 года, из них 231 мужчина и 320 женщин. Выборка 2 состояла из данных исследования новой группы участников в числе 333 человек. Группа участников исследования включала здоровых лиц и пациентов с клинически верифицированным диагнозом депрессии разной степени тяжести. Возраст участников составил 24–53 года, из них 145 мужчин и 189 женщин.
Методология определения пороговых критериев выраженности депрессии в шкале HDRSm-10 состояла в следующем.
Поскольку клиническая психометрическая шкала направлена на измерение латентного психопатологического конструкта, измерение последнего всегда включает случайную ошибку. При многократных исследованиях одного и того же участника исследования значения полученных оценок будут отличаться друг от друга в диапазоне, который определяется случайной ошибкой измерения. Случайная ошибка в каждом очередном исследовании также принимает неодинаковые значения, образуя дисперсию ошибки s2error [7].
Стандартное отклонение случайной ошибки получило название стандартной ошибки измерения (SEM): √s2error (1), где s2error – дисперсия случайной ошибки [7].
Разделение шкалы на значимые метрические уровни, границы которых образуют пороговые критерии, основывается на определении статистически значимых метрических различий между шкальными оценками. Если оценки метрически различаются, они относятся к различным метрическим уровням выраженности конструкта и являются научно обоснованными критериями их интерпретации. Если оценки статистически не различаются, то они соответствуют одному и тому же метрическому уровню выраженности конструкта, и, следовательно, их критерии интерпретации одинаковы. Статистические различия между оценками определяются с помощью стандартной ошибки разницы между ними (SEMdif) c заданным уровнем вероятности. Значение SEMdif рассчитывается на основе значения SEM каждой из оценок, между которыми определяется разница.
Пусть нам необходимо определить стандартную ошибку разницы между любыми 2 шкальными оценками Xi и Хj. Каждая оценка представляет собой переменную, принимающую различные значения при многократных исследованиях в диапазоне, образуемом своей стандартной ошибкой измерения: SEMXi для оценки Xi и SEMXj для оценки Хj. Разность между этими оценками (Хj - Хi) также представляет собой переменную, значение которой изменяется при многократных исследованиях в диапазоне стандартной ошибки разности между этими оценками (SEMXj-Xi). Задача состоит в определении значения SEMXj-Xi. Поскольку SEM представляет собой стандартное отклонение случайной ошибки шкальной оценки, то SEMXj-Xi является стандартным отклонением случайной ошибки разности между шкальными оценками Xi и Хj: SEMXj-Xi = √s2error (Xj-Xi) (2), где s2error (Xj-Xi) – дисперсия случайной ошибки разности оценок Xi и Хj. Как известно, дисперсия разности 2 переменных равна сумме дисперсий этих 2 переменных. Следовательно, формула расчета дисперсии ошибки разности оценок Xi и Хj будет иметь вид: s2error (Xj-Xi) = s2error (Xi) + s2error (Xj) (3). Отсюда значение SEMXj-Xi можно определить по формуле: SEMXj-Xi = √s2error (Xj-Xi) = √s2error (Xi) + s2error (Xj) = √SEM2Xi + SEM2Xj(4). Таким образом, стандартная ошибка разности 2 оценок равна квадратному корню суммы квадратов стандартных ошибок измерения каждой из этих оценок. Следовательно, для расчета стандартной ошибки разности между оценками (SEMdif) достаточно знать значения стандартных ошибок измерения этих оценок (SEM).
Итак, если разность между оценками с приемлемым уровнем статистической значимости превышает величину стандартной ошибки этой разницы, то с высокой долей вероятности можно утверждать о принадлежности данных оценок разным уровням выраженности измеряемого конструкта. Приемлемый уровень статистической значимости определяется допустимой вероятностью отвержения нулевой гипотезы. В данном случае нулевая гипотеза состоит в том, что статистически значимое превышение разности 2 оценок над величиной стандартной ошибки измерения этой разности не будет свидетельствовать о действительных различиях между оценками. В исследованиях, посвященных разработке критериев интерпретации, для определения уровня статистической значимости различий между оценками эмпирически принята вероятность, равная 95% [2]. Распределение случайной ошибки подчиняется нормальному закону. Это дает возможность использования значений стандартизованных Z-оценок в качестве критериев статистической значимости разности между оценками. Каждому значению плотности вероятности соответствует определенная Z-оценка. Для вероятности 95% значение Z-оценки равно 1,96 [2]. Таким образом, разность между 2 шкальными оценками Xi и Хj будет статистически значимой, если соблюдается следующее условие:
Xj-Xi/√SEM2Xi+SEM2Xj >1,96. (5). Преобразуем данное выражение в более удобную форму: Xj-Xi>1,96√SEM2Xi+SEM2Xj (6). Выражение (6) можно определить как метрическое условие, определяющее принадлежность 2 шкальных оценок к статистически разным метрическим уровням с 95% вероятностью. Практическое использование данного метрического условия на основе модели Раша проводится следующим образом. Как мы уже отмечали выше, в ходе психометрического анализа в метрической системе Раша строится равноинтервальная шкала, на которой каждая суммарная оценка имеет свою метку, выраженную в логитах. Для каждой метки рассчитывается индивидуальная ошибка измерения. Метрическое условие (6) используется для разделения шкалы логитов на метрические уровни. Логиты, образующие границы уровней, являются пороговыми критериями. Каждому критерию, выраженному в логитах, соответствует определенная суммарная оценка. Процесс разделения шкалы на уровни проводится, начиная с метки шкалы, эквивалентной нулевой суммарной оценке. Данная метка соответствует оценке Xi в метрическом условии. Далее условие последовательно проверяется для каждой последующей метки шкалы. При этом в правую часть неравенства подставляются значения соответствующих ошибок измерения. Как только значение левой части неравенства станет больше правой, первый метрический уровень определен. При этом суммарная оценка шкалы, эквивалентная метке шкалы, выступающей в качестве оценки Xj, будет определена как нижний пороговый критерий 2-го метрического уровня. Предшествующая ей оценка представляет верхний пороговый критерий 1-го уровня. Далее в метрическое условие в качестве оценки Xi подставляется метка шкалы, образовавшая нижний пороговый критерий 2-го метрического уровня, и процесс повторяется до самой последней метки, которая эквивалентна максимальной суммарной оценке по шкале.
Клиническая верификация пороговых метрических критериев проводилась путем статистического анализа таблиц сопряженности клинических и метрических критериев. При этом строки таблицы включали частоты клинических критериев выраженности конструкта по Международной классификации болезней 10-го пересмотра (МКБ-10), столбцы таблицы содержали частоты метрических критериев. В ячейках на пересечении строк и столбцов локализовались совпадающие частоты. Статистический анализ заключался в определении максимальной частоты каждого клинического критерия, которая совпадала с максимальной частотой определенного метрического критерия. Метрический критерий, совпавший по максимальной частоте с определенным внешним клиническим критерием, приобретал свойство клинической интерпретируемости, соответствующий данному внешнему критерию. Если внешнему клиническому критерию по максимальным частотам соответствовали 2 и более метрических критерия, то они объединялись в один общий критерий, имеющий 2 метрических уровня. В качестве статистических критериев определения значимой максимальной частоты использовался точный метод Фишера (ТМФ) [8].
Оценка диагностической эффективности пороговых критериев осуществлялась путем оценки степени согласованности классификации испытуемых по степени тяжести депрессии, выполненной на основе метрических критериев, с классификацией, построенной на основе клинических критериев МКБ-10. Оценка степени соответствия классификаций проводилась с помощью статистических критериев c2, процента рассогласованности классификаций, индекса каппа Коэна, индекса выраженности эффекта (effect-size) V Крамера [9]. Оценка эффективности критериев классификации проводилась на данных исследования выборки 1 и выборки 2. Оцениванию подвергались новые критерии интерпретации в сравнении с существующими критериями оригинальной 17-пунктовой шкалы HRSD. Для проведения сравнительного анализа использовались 2 набора оригинальных пороговых критериев. Первый набор состоял из традиционных устоявшихся пороговых оценок, второй набор включал пороговые оценки, рекомендуемые Американской психиатрической ассоциацией (American Psychiatric Association – APA) [10]. Пороговые критерии обоих наборов представлены в табл. 1.

Результаты
 В табл. 2 представлены все оценки шкалы HDRSm-10, разделенные на метрические уровни.
В табл. 2 представлены все оценки шкалы HDRSm-10, разделенные на метрические уровни.Как следует из данных табл. 2, в шкале HDRSm-10 на основе модели Раша выделяются 7 метрических уровней. Это означает, что данная шкала с 95% вероятностью дифференцирует 7 степеней выраженности депрессии. Метрические уровни на схеме расположены последовательно сверху вниз и отражают возрастающие степени выраженности депрессии.
Эффективное практическое применение модифицированной шкалы HDRSm-10 требует согласования метрических критериев выраженности депрессии с внешними клиническими критериями. Клиническая валидизация метрических критериев интерпретации проводилась с помощью статистического анализа таблиц сопряженности классификации участников исследования на основе внешнего клинического критерия (по МКБ-10) и с классификацией на основе метрических критериев шкалы HDRSm-10. В табл. 3 представлены частоты метрических уровней, определенных в модифицированной шкале HDRSm-10, в сопряжении с частотами клинических уровней в группах участников.
Исходя из практической целесообразности, метрические и клинические уровни должны быть согласованы таким образом, чтобы каждый метрический уровень соответствовал только одному клиническому. Это обеспечивает понятность и удобство интерпретации метрических критериев с клинической точки зрения. Как следует из анализа данной таблицы, в каждом столбце обнаруживается частота, имеющая максимальное значение. Это означает, что каждый метрический уровень эквивалентен только одному клиническому уровню.
Анализ данных табл. 3 позволяет выполнить согласование метрических и клинических уровней, представленных в табл. 2. Первый метрический уровень (от 0 до 4 баллов) соответствует уровню отсутствия депрессии. Второй метрический уровень (от 5 до 9 баллов) согласуется с легкой степенью депрессии. Третий (10–14 баллов) и четвертый (15–19 баллов) метрические уровни соответствуют средней степени тяжести депрессии, установленной по клиническому критерию. Последние 3 метрических уровня (20–23, 24–27, 28 и более баллов) эквивалентны клинически диагностируемой тяжелой степени депрессии.
Таким образом, метрические критерии шкалы HDRSm-10, определенные на основе модели Раша, эффективно согласуются с клиническими уровнями выраженности депрессии. При этом клинический уровень умеренно выраженной депрессии включает 2 метрически и статистически отличающихся друг от друга подуровня. Клинический уровень тяжелой депрессии включает 3 дифференцированных метрических подуровня. Наличие нескольких метрических уровней в рамках одного клинического позволяет точнее и валиднее оценивать изменение выраженности депрессии в динамике терапии.
Сравнительная оценка диагностической эффективности оригинальных и новых критериев интерпретации проводилась на основе определения степени согласованности критериев оригинальной и модифицированной шкал с клиническими критериями оценки тяжести депрессии в соответствии с МКБ-10. Для оценки степени согласованности использовались следующие статистические критерии: c2, индекс V Крамера, показатель рассогласованности в процентах, индекс Каппа. Оценка диагностической эффективности проводилась дважды на разных выборках данных (выборка 1 и выборка 2). Значения показателей диагностической эффективности представлены в табл. 4. В процессе оценки эффективности критериев шкалы HDRSm-10 несколько метрических уровней, эквивалентных одному и тому же клиническому уровню (см. табл. 3), объединялись в данный клинический уровень. В частности, третий и четвертый метрические уровни были объединены в один уровень умеренной степени тяжести депрессии, четвертый, пятый и шестой метрические уровни объединены в один уровень тяжелой степени депрессии. Первый и второй метрические уровни представляли соответственно уровень отсутствия депрессии и легкую степень депрессии.
Оценка показателей, приведенных в табл. 4, обнаруживает выраженные различия в диагностической эффективности пороговых критериев оригинальной шкалы HDRS и критериев модифицированной шкалы. Пороговые критерии оригинальной шкалы показали выраженную рассогласованность с клиническими критериями МКБ-10. Степень рассогласования традиционных критериев с клиническими данными в обеих выборках превышает 40%, критериев АРА – от 30 до 38%. Отмечаются достоверные различия по критерию c2 в обеих выборках (p<0,0001). Эффект различий (effect-size) между классификациями по значениям индекса V Крамера составил высокую степень выраженности. Значения коэффициента Каппа для критериев оригинальной шкалы также соответствуют невысокой согласованности с клиническими критериями. Полученные данные свидетельствуют о низкой диагностической эффективности как традиционных, так и рекомендованных АРА пороговых критериев оценки тяжести депрессии оригинальной шкалы HDRS.

Критерии модифицированной шкалы, напротив, показали высокую эффективность при сопоставлении с клиническими критериями. Степень рассогласования с клиническими данными составляет менее 14%. Значения индекса Каппа отражают достаточно высокий уровень согласованности. Значения критерия c2 обнаруживают отсутствие достоверных различий с классификацией по клиническим критериям в обеих выборках. Значения индекса выраженности эффекта V (effect-size) свидетельствуют о слабой рассогласованности в выборке 1 (V=0,06) и об отсутствии таковой в выборке 2 (V=0,05).
Таким образом, на основании проведенного исследования можно сделать следующие выводы.
1. Метрические пороговые критерии оценки психопатологического конструкта, разработанные на основе модели Раша, обладают высокой степенью стабильности и воспроизводимости, эффективно согласуются с клиническими данными.
2. Разработанная нами на основе модели Раша модифицированная шкала оценки депрессии HDRSm позволяет оценить 7 метрических уровней выраженности депрессии, хорошо согласуется с клиническими данными и значительно превосходит по своим диагностическим свойствам оригинальную шкалу HRSD.
Сведения об авторе
Ассанович Марат Алиевич – канд. мед. наук, доц., зав. каф. медицинской психологии и психотерапии ГрГМУ.
E-mail: 70malas@gmail.com

